Quick Sort
아무리 뛰어난 정렬 알고리즘(:12)을 개발한다고 하더라도, 데이터의 갯수가 N이면 O(NlogN)보다 더 좋을 수
없다는 것이 증명되어 있다.
즉 정렬알고리즘의 lower bound는 O(NlogN)이다.
단 최대값이 정해져 있는 데이터라면 counting 방식을 쓸수 있고 - counting sort, bucket sort, radix sort - 이 경우 O(n)이 보장될 것이다.
- 주어진 데이터 목록에서 임의의 원소를 고른다. 이 원소를 피봇이라 한다.
- 피봇을 기준으로 피봇의 앞에는 피봇보다 작은 숫자가 오도록 하고, 피봇 뒤에는 피봇보다 큰 원소가 오도록한다. 필요할 경우 피봇은 움지일 수 있다.
- 1,2의 과정을 재귀수행한다. 한번의 피봇이 선택되어서 분할이 이루어질 때마다. 반드시 고정되는 값이 생성이 되므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

void quickSort(int numbers[], int array_size);
void q_sort(int numbers[], int left, int right);
void quickSort(int numbers[], int array_size)
{
q_sort(numbers, 0, array_size -1);
}
void q_sort(int numbers[], int left, int right)
{
int pivot, l_hold, r_hold;
l_hold = left;
r_hold = right;
pivot = numbers[left]; // 0번째 원소를 피봇으로 선택
while (left < right)
{
// 값이 선택한 피봇과 같거나 크다면, 이동할 필요가 없다
while ((numbers[right] >= pivot) && (left < right))
right --;
// 그렇지 않고 값이 피봇보다 작다면,
// 피봇의 위치에 현재 값을 넣는다.
if (left != right)
{
numbers[left] = numbers[right];
}
// 왼쪽부터 현재 위치까지 값을 읽어들이면서
// 피봇보다 큰 값이 있다면, 값을 이동한다.
while ((numbers[left] <= pivot) && (left < right))
left ++;
if (left != right)
{
numbers[right] = numbers[left];
right --;
}
}
// 모든 스캔이 끝났다면, 피봇값을 현재 위치에 입력한다.
// 이제 피봇을 기준으로 왼쪽에는 피봇보다 작거나 같은 값만 남았다.
numbers[left] = pivot;
pivot = left;
left = l_hold;
right = r_hold;
// 재귀호출을 수행한다.
if (left < pivot)
q_sort(numbers, left, pivot - 1);
if (right > pivot)
q_sort(numbers, pivot+1, right);
}
int main(int argc, char **argv)
{
int data[] = {3,7,8,5,2,1,9,5,4};
int i;
quickSort(data, 9);
for (i =0; i < 9; i++)
{
printf("%d\n", data[i]);
}
}
Quicksort is a very efficient sorting algorithm invented by C.A.R. Hoare. It has two phases:
- the partition phase and
- the sort phase.
This makes Quicksort a good example of the divide and conquer strategy for solving problems. (You've already seen an example of this approach in the binary search procedure.) In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions, ie we divide the problem into two smaller ones and conquer by solving the smaller ones. Thus the conquer part of the quicksort routine looks like this:
quicksort( void *a, int low, int high )
{
int pivot;
/* Termination condition! */
if ( high > low )
{
pivot = partition( a, low, high );
quicksort( a, low, pivot-1 );
quicksort( a, pivot+1, high );
}
}
|
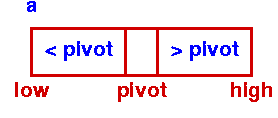 Initial Step - First Partition |
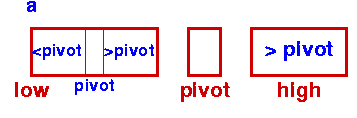 Sort Left Partition in the same way |
To do this, we choose a pivot element and arrange that all the items in the lower part are less than the pivot and all those in the upper part greater than it. In the most general case, we don't know anything about the items to be sorted, so that any choice of the pivot element will do - the first element is a convenient one.
As an illustration of this idea, you can view this animation, which shows a partition algorithm in which items to be sorted are copied from the original array to a new one: items smaller than the pivot are placed to the left of the new array and items greater than the pivot are placed on the right. In the final step, the pivot is dropped into the remaining slot in the middle.
Quicksort
Quicksort is a fast sorting algorithm, which is used not only for educational purposes, but widely applied in practice. On the average, it has O(n log n) complexity, making quicksort suitable for sorting big data volumes. The idea of the algorithm is quite simple and once you realize it, you can write quicksort as fast as bubble sort.
Algorithm
The divide-and-conquer strategy is used in quicksort. Below the recursion step is described:- Choose a pivot value. We take the value of the middle element as pivot value, but it can be any value, which is in range of sorted values, even if it doesn't present in the array.
- Partition. Rearrange elements in such a way, that all elements which are lesser than the pivot go to the left part of the array and all elements greater than the pivot, go to the right part of the array. Values equal to the pivot can stay in any part of the array. Notice, that array may be divided in non-equal parts.
- Sort both parts. Apply quicksort algorithm recursively to the left and the right parts.
Partition algorithm in detail
There are two indices i and j and at the very beginning of the partition algorithm i points to the first element in the array and j points to the last one. Then algorithm moves i forward, until an element with value greater or equal to the pivot is found. Index j is moved backward, until an element with value lesser or equal to the pivot is found. If i ≤ j then they are swapped and i steps to the next position (i + 1), j steps to the previous one (j - 1). Algorithm stops, when i becomes greater than j.
After partition, all values before i-th element are less or equal than the pivot and all values after j-thelement are greater or equal to the pivot.
Example. Sort {1, 12, 5, 26, 7, 14, 3, 7, 2} using quicksort.
Notice, that we show here only the first recursion step, in order not to make example too long. But, in fact, {1, 2, 5, 7, 3} and {14, 7, 26, 12} are sorted then recursively.
Why does it work?
On the partition step algorithm divides the array into two parts and every element a from the left part is less or equal than every element b from the right part. Also a and b satisfy a ≤ pivot ≤ binequality. After completion of the recursion calls both of the parts become sorted and, taking into account arguments stated above, the whole array is sorted.Complexity analysis
On the average quicksort has O(n log n) complexity, but strong proof of this fact is not trivial and not presented here. Still, you can find the proof in [1]. In worst case, quicksort runs O(n2) time, but on the most "practical" data it works just fine and outperforms other O(n log n) sorting algorithms.
Code snippets
Partition algorithm is important per se, therefore it may be carried out as a separate function. The code for C++ contains solid function for quicksort, but Java code contains two separate functions for partition and sort, accordingly.
Java
int partition(int arr[], int left, int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j) {
while (arr[i] < pivot)
i++;
while (arr[j] > pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
return i;
}
void quickSort(int arr[], int left, int right) {
int index = partition(arr, left, right);
if (left < index - 1)
quickSort(arr, left, index - 1);
if (index < right)
quickSort(arr, index, right);
}
C++
void quickSort(int arr[], int left, int right) {
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
/* partition */
while (i <= j) {
while (arr[i] < pivot)
i++;
while (arr[j] > pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
/* recursion */
if (left < j)
quickSort(arr, left, j);
if (i < right)
quickSort(arr, i, right);
}
Reference :
댓글 없음:
댓글 쓰기